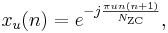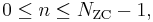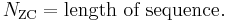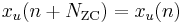Zadoff–Chu sequence

A Zadoff–Chu sequence is a complex-valued mathematical sequence which, when applied to radio signals, gives rise to an electromagnetic signal of constant amplitude, whereby cyclically shifted versions of the sequence imposed on a signal result in zero cross-correlation with one another at the receiver. A generated Zadoff–Chu sequence that has not been shifted is known as a "root sequence".

The sequence then exhibits the useful property that cyclically shifted versions of itself are orthogonal to one another, provided, that is, that each cyclic shift, when viewed within the time domain of the signal, is greater than the combined propagation delay and multi-path delay-spread of that signal between the transmitter and receiver.

The complex value at each position (n) of each root Zadoff–Chu sequence (u) given by

x_u(n)=e^{-j\frac{\pi un(n%2B1)}{N_\text{ZC}}}, \,

where

0 \le n \le N_\text{ZC}-1, \,
N_\text{ZC} = \text{length of sequence}.\,

Zadoff–Chu sequence is known as a CAZAC sequence (constant amplitude zero autocorrelation waveform).

It is named after Solomon A. Zadoff and D. C. Chu.

Properties of Zadoff-Chu sequences

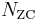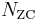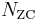1. They are periodic with period N_\text{ZC} if N_\text{ZC} is prime.

x_u ( n %2B N_{\text{ZC}} )= x_u(n)

2. Given N_\text{ZC} is prime, Discrete Fourier Transform of Zadoff–Chu sequence is another Zadoff–Chu sequence conjugated, scaled and time scaled.

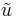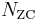X_{u}[k]= x_{u}^{*}(\tilde{u}k) X_{u}[0] where \tilde{u} is the multiplicative inverse of u modulo N_\text{ZC} .

3. The autocorrelation of a prime length Zadoff–Chu sequence with a cyclically shifted version of itself also has zero auto-correlation, i.e., it is non-zero only at one instant which corresponds to the cyclic shift.

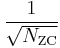
4. The cross correlation between two prime length Zadoff–Chu sequences, i.e. different u , is constant \frac{1}{\sqrt{N_\text{ZC}}}

Usages

Zadoff–Chu sequences are used in the 3GPP LTE Long Term Evolution air interface in the Primary Synchronization Signal (PSS) (so-called primary synchronization channel), random access preamble (PRACH), HARQ ACK/NACK responses (PUCCH) and sounding reference signals (SRS). By assigning orthogonal Zadoff-Chu sequences to each LTE eNodeB and multiplying their transmissions by their respective codes, the cross-correlation of simultaneous eNodeB transmissions is reduced, thus reducing intra-cell interference and uniquely identifying eNodeB transmissions. Zadoff-Chu sequence improve over the Walsh–Hadamard codes used in UMTS because they result in a constant-amplitude output signal, reducing the cost and complexity of the radio's power amplifier.[1]

References

  1. ^ Evolved Cellular Network Planning and Optimization for UMTS and LTE, Lingyang Song and Jia Shen, CRC Press, 2011, New York